圆周率被界说为圆的周长和直径的比值，频繁用“π”来示意，它是通盘的圆所共有的一个数学常数，也即是说白虎 自慰，岂论一个圆的大小何如，其周长和直径的比值齐保合手不变，是一个固定的值。

念念要知说念圆周率到底是几许，最通俗的关节即是，径直测量出一个圆的周长和直径，然后再作念一个除法就不错了，但这么的关节却有一个问题，那即是岂论什么样的测量，齐是有舛错的，而舛错的存在，就会导致咱们无法精准地盘算出圆周率。是以咱们需要在不进行测量的前提下，通过纯表面的推导来盘算出圆周率的精准值。

骨子上，从公元前三世纪的古希腊数学家阿基米德启动，东说念主类就一直在执着地通过表面来盘算圆周率。

最新国内偷拍凹凸视频在线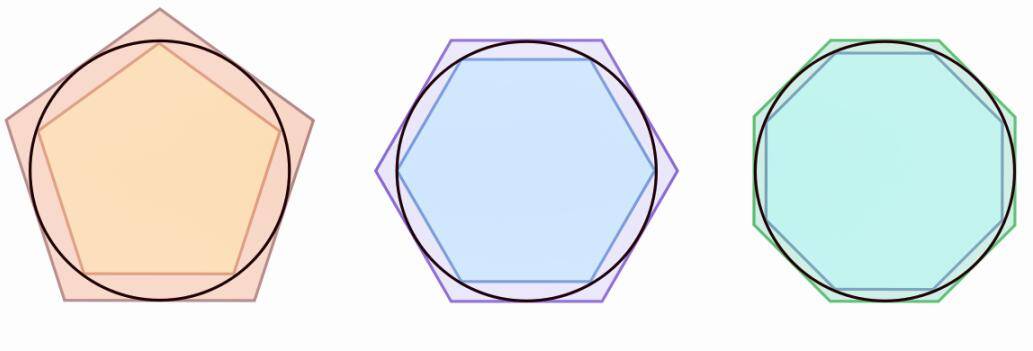

阿基米德的关节不错通俗地表情为：在一个圆的里面和外部永诀画一个内接正六边形和一个外接正边形，这么就不错通过勾股定理盘算出圆周率在3至4之间，在此基础上，只需要合手续增增多边形的边数，就不错取得越来越接近好意思满的圆，进而盘算出越来越精准的圆周率。

阿基米德使用了这种关节盘算到边数为96的正多边形，他的盘算着力是，圆周率在3.140845至3.142857之间。

在东说念主类盘算圆周率的历史中，我国的数学家留住了浓墨重彩的一笔，公元263年，我国数学家刘徽提议了著明的“割圆术”，这种关节不错通俗地表情为，通过“割圆”的面容合手续增加圆内接正多边形的边数，使其面积抑止面对圆的面积，进而盘算出越来越精准的圆周率。

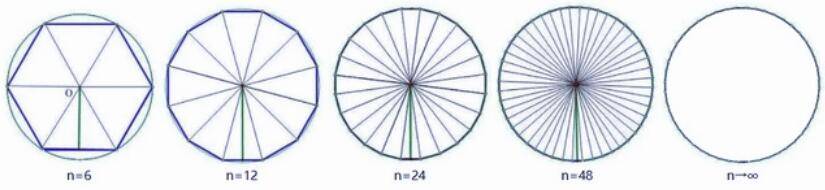
通过“割圆术”，刘徽盘算出圆周率的值粗略为3.1416，而在公元480年掌握，我国数学家祖冲之则进一步将圆周率的盘算推向了新的高度，他应用“割圆术”，一举将圆周率精准到一丝点后7位白虎 自慰，也即是咱们所练习的“3.1415926至3.1415927之间”，而他的盘算着力，则保合手了近千年的宇宙记录。